Richard Weber
Talk to Sidney Sussex College mathematicians (6.30pm, Old Library) November 6, 2012
You have mislaid \(k\) objects (such as your keys, wallet, mobile phone, etc). Each is lost in one of \(n\) (\(>k\)) locations (such as coat pocket, desk drawer, under bed, gym locker, etc.). It will cost \(c_i\) to search location \(i\) and you want to minimize the expected cost in finding all your objects. “Sod’s law” predicts that the objects are distributed amongst the locations with whatever probability distribution makes your task most difficult. What is this “Sod’s law” distribution? In what order should you search the locations? I will discuss this and some similar problems. Another cute one is this: “In how many places should a forgetful squirrel hide his nuts?”
There are also many worthwhile practical search problems, like “rescue at sea”, “researching for a cancer cure”, and “oil exploration”.
The King of Spain has hidden treasure on \(n\) Caribbean islands \(1,\dotsc,n\) in caches of values \(r_1,\dotsc,r_n\).
A band of pirates, starting from their home on island \(0\), sail to \(m\) (\(\leq n\)) islands in sequence \(i_1,i_2,\dotsc,i_m\), searching for treasure. They need not visit all the islands.
The pirates’ payoff depends on how much treasure they steal, and their search cost (from sailing and digging), say \[ r_{i_1}+\cdots+r_{i_m}-(c_{0}^{i_1}+c_{0,i_1}^{i_2}+\cdots +c_{0,i_1\dotsc,i_{m-1}}^{i_m}). \] Note that the cost of collecting the treasure on island \(i_j\) depends on the sequence of islands previously visited. This generality includes models in which pirates
must tour the islands in a single ship, or
can establish bases on visited islands and expand their search from any of these.
If the \(r_i\) are known, or can be modelled as independent random variables, then the pirates face a sort of travelling saleman problem.
But suppose the king is hiding a total treasure of value \(r\) and can freely choose how to split it and hide it (with \(r=r_1+\cdots+r_n\)).
The king’s payoff might be
the negative of the pirates’ payoff (giving a zero-sum game), or
\(-(r_{i_1}+\cdots+r_{i_m})\), or
1 or 0 as \((r_{i_1}+\cdots+r_{i_m})\leq s\) or \(> s\), respectively.
What is the optimal hiding strategy for the king? In what order should the pirates visit the islands? At what \(m\) should they stop searching? Does it help the king to re-hide the treasure at intermediate stages?
This is a rich model, with many interesting special cases. For example, we might suppose the sizes of the caches are given and the king’s task it to decide how to allocate them to the islands.
The talk will look at a few interesting special cases.
Suppose costs are as follows. Then pirates will visit exactly \(m\) islands. \[ c_{0,i_1\dotsc,i_{j-1}}^{i}= \left\{\begin{array}{cc} 0, & j \leq m\\[8pt] \infty, & j > m. \end{array}\right. \]
The king wishes to maximize that probability that they steal no more than \(s\).
Ruckle’s conjecture. The optimal strategy for the king is (for some integer \(k\)) to hide his treasure on \(k\) randomly chosen islands in equal caches of size \(r/k\).
In other words, it is never optimal to use more than one cache size.
The optimal \(k\) depends on \(r\), \(s\), \(n\) and \(m\).
The pirates visit a randomly chosen set of \(m\) islands.
The king hides the treasure in \(k\) equal caches.
The costs are \(c_{0,i_1\dotsc,i_{j-1}}^{i}=c_{i}\).
Assume that these are so small that the pirates will continue until they have found all the treasure.
The game is about \(k\) objects hidden in \(n\) locations, \(n> k\).
The cost of searching location \(i\) is \(c_i\).

Task: minimize the expected cost of finding all \(k\) objects.
“Dumb” searcher would simply choose a permutation of \(1,2,\dotsc,n\) and search locations in that order until all \(k\) objects are found.
“Smart” searcher might adjust his choice of where to search next on the basis of how many objects are still to be found and which locations have not yet been searched.
\[ \sum_{\{i_1,i_2,\dotsc,i_k\}\subset\{1,2,\ldots,n\}}p({i_1,\dotsc,i_k})=1. \]
For example, if locations are chosen at random, so \(p({i_1,\dotsc,i_k})=1/\binom{n}{k}\), it will be optimal to search the locations in increasing order of the \(c_i\).
But probably the objects are not hidden at random.
Sod’s Law says that buttered toast will land butter side down! :(
Sod’s Law says that objects will be hidden with whatever probability distribution makes the searcher’s task most difficult!
What is the Sod’s Law distribution in Lidbetter’s problem?
Digression:
Sod’s First Law
When a person attempts a task, he or she will be thwarted in that task by the unconscious intervention of some other presence (animate or inanimate)
Task Completion Theorem
Nevertheless, some tasks are completed, since the intervening presence is itself attempting a task and is, of course, subject to Sod’s law.
Sod’s Second Law
Sooner or later, the worst possible set of circumstances is bound to occur.
Sod’s Other Law
The degree of failure is in direct proportion to the effort expended and need for success.
A two-person zero-sum game.
Hider: hides the object in location \(i\) (\(\in\{1,2\}\)).
Searcher: starts by searching location \(j\) (\(\in\{1,2\}\)).
We define the searcher’s payoff as the cost saved from locations that he does not search.
Payoff matrix (with searcher being the row player) is \[ A=(a_{ij})=\begin{pmatrix} c_2 & 0\\ 0 & c_1 \end{pmatrix}. \]
Searcher’s optimal mixed strategy is \[ p^\top=\left(\frac{c_1}{c_1+c_2},\frac{c_2}{c_1+c_2}\right),\quad\text{and then } p^\top A = (v,v) \] where \[ v=\frac{c_1c_2}{c_1+c_2}. \] Since \(A=A^\top\) we also have \[ Ap = \begin{pmatrix}v\\v\end{pmatrix} \] and so this is also the hiders’s optimal strategy.
Hider: w.p. \(c_i/(c_1+c_2)\) hide the object in location \(i\).
Searcher: w.p. \(c_i/(c_1+c_2)\) start by searching location \(i\).
Value of the game is \(v=c_1c_2/(c_1+c_2)\).
Suppose hider uses the same strategy as above i.e. hides in location \(i\) w.p. \(c_i/C\), where \(C=\sum_i c_i\).
What is the searcher’s expected cost if he searches in order \(1,2,\dotsc,n\)?
Probability searcher does not search location \(j\) is the probability that the object is hidden in one of the locations \(1,\dotsc,j-1\). So
Expected reward for the searcher is \[ v := \sum_{j=2}^n \left(\frac{c_1+\cdots+c_{j-1}}{C}\right)c_j = \frac{1}{C}\sum_{i<j} c_ic_j. \] This is the same for all possible labellings of the locations, i.e., for all search orders.
So if the hider uses this mixed strategy then \(p^\top A = v(1,1,\dotsc,1)\).
\(\implies\) The hider can ensure that the searcher has reward no more than \(v\).
Suppose he starts by searching location \(i\) w.p. \(c_i/C\) and then searches randomly.
Let’s see what happens if the searcher starts by searching location \(1\) and the object is in location \(j\).
\(j=1\): searcher pays \(c_1\).
\(j\neq 1\): searcher pays at least \(c_j+c_1\).
For \(k\not\in\{1,j\}\), location \(k\) will be searched if, while searching \(\{2,3,\ldots,n\}\) in random order, \(k\) is searched before \(j\).
Clearly this has probability \(1/2\). So expected cost is \[ c_1+c_j+\frac{1}{2}\sum_{k\neq 1,j}c_k=\frac{c_1+c_j+C}{2}. \]
So payoff matrix (cost of locations not searched) is \[ A= \begin{pmatrix} C-c_1 & \frac{C-c_1-c_2}{2} & \cdots & \frac{C-c_1-c_n}{2}\\ \frac{C-c_2-c_1}{2} & C-c_2 & \cdots & \frac{C-c_2-c_n}{2}\\ \vdots & \vdots &\ddots &\vdots\\ \frac{C-c_n-c_1}{2} & \frac{C-c_n-c_2}{2} &\cdots&C- c_n \end{pmatrix} \]
Since \(A\) is symmetric, \(Ap=v1\) and hence \(p\) (with the extended notion of searching at random after the first location) ensures that the searcher’s reward is at least \(v\).
Hider: w.p. \(c_i/C\) hide the object in location \(i\).
Searcher: w.p. \(c_i/C\) start by searching location \(i\), and then search in random order until all objects are found.
\[ v = \frac{1}{C}\sum_{i<j} c_ic_j. \]
Define the symmetric sum \[ S_k = \sum_{\{i_1,i_2,\dotsc,i_k\}\subset\{1,2,\ldots,n\}}c_{i_1}\cdots c_{i_k}, \] i.e., the sum of all products of \(k\) distinct elements of \(\{c_1,\dotsc,c_n\}\).
\(C=S_1=\sum_i c_i\).
Claim:
Hider: w.p. \((c_{i_1}\cdots c_{i_k})/S_k\) hide the objects in locations \(i_1,\dotsc,i_k\). (This is Sod’s Law)
Searcher: w.p. \((c_{i_1}\cdots c_{i_k})/S_k\) start by searching locations \(i_1,\dotsc,i_k\), and then search remaining locations in random order until all objects are found.
Suppose hider uses the above strategy, and searcher searches locations in the order \(1,2,\dotsc,n\).
Location \(i\) (\(i>k\)) is not searched if the objects were hidden amongst locations \(1,\dotsc,i-1\). Hence expected cost is
\[ \begin{aligned} v &:= \sum_{i=k+1}^n c_i\sum_{\{i_1,i_2,\dotsc,i_k\}\subset\{1,2,\ldots,i-1\}}\frac{c_{i_1}\cdots c_{i_k}}{S_k}\\[12pt] &= \frac{S_{k+1}}{S_k}. \end{aligned} \]
This is independent of the labelling, so the hider can ensure that a dumb searcher’s average reward is no more than \(v\).
In fact, this also ensures that a smart searcher’s average reward is no more than \(v\) — essentially because at all stages of search the remaining objects are still hidden in the unsearched locations according to Sod’s Law.
To finish proof of the claim we must also show that the searcher can obtain reward of at least \(v\). This is accomplished by showing he can do this even when he is dumb, and restricts himself to searching at random after he has searched \(k\) locations.
So
a pure strategy for the hider is a set of \(k\) locations, say \(H\), in which he hides the objects, and
a pure strategy for the searcher is a set of \(k\) locations, say \(K\), that he searches first, before subsequently searching at random.
All locations in the set \(H\cup K\) will be searched. The payoff matrix is \[ a(H,K) = \bar q \sum_{j\not\in H\cup K}c_j \] where \(\bar q\) is the probability that having searched all locations in \(K\) the searcher does not search location \(j\not\in H\cup K\) before finding all the items in \(H\setminus K\). The probability \(\bar q\) depends only on the size of \(H\setminus K\) relative to \(n-k\), i.e. on the number of locations in \(H\) that are not in \(K\).
Since \(|H\setminus K|=|K\setminus H|\) this means that \(a(H,K) =a(K,H)\).
So, as in the \(k=1\) case, the payoff matrix \(A\) is symmetric.
This means that the optimal hider and searcher strategies are identical, as described above, the searcher obtains expected payoff of at least \(v\), and so the value of the game is \(v\).
Note: We said that the searcher restricts himself to searching at random after he has searched \(k\) locations. But there is no advantage for him in relaxing this restriction.
So far we have made the following assumptions.
The hider is dumb (he chooses \(k\) hiding locations and leaves the objects there).
The searcher is dumb (he chooses an order in which to search the locations and does not revise that order as his search proceeds).
Suppose both are smart and can revise their strategies dynamically.
The hider can re-hide the remaining objects, and the searcher can pick where to search next, both as functions of when and where objects have been found so far.
Theorem. The value of this game is \(S_{k+1}/S_k\), i.e. the same as with a dumb hider and dumb (or smart) searcher.
Proof.
Let \(S_k^i\) denote the \(k\)-symmetric sum of the set of elements \(\{c_1,\dotsc,c_n\}\setminus c_i\) (i.e. excluding the \(i\)th location).
We prove the theorem by induction. Base of induction can be \(k=1,n=2\).
Suppose that the hider starts by hiding the objects in the set of locations \(H\), with probability \(p_H\). If the searcher searches location \(i\) then his expected payoff is \[ A(i):=\sum_{H:i\in H}p_H \frac{S_k^i}{S_{k-1}^i} +\sum_{H:i\not\in H}p_H \frac{S_{k+1}^i}{S_{k}^i}. \] Now if \(p\) is Sod’s Law then \[ \sum_{H:i\in H}p_H = \frac{c_i S_{k-1}^i}{S_k},\quad\text{and } \sum_{H:i\not\in H}p_H = \frac{S_{k}^i}{S_k}. \] This easily gives \(A(i)=S_{k+1}/S_k\).
On the other hand, suppose the hider starts by hiding the objects in the set of locations \(H\). If the searcher starts by searching location \(i\) with probability \(p_i\), then \[ A(H):= \sum_{i\in H}p_i\frac{S_k^i}{S_{k-1}^i} +\sum_{i\not\in H}p_i\frac{S_{k+1}^i}{S_{k}^i}. \]
By considering two sets \(H\) and \(H'\) which differ only in that \(H\) includes \(i\) and \(H'\) contains \(j\), we see that \(A(H)\) is independent of \(H\) if \(p_i\) is chosen so that
\[ p_i\left(\frac{S_k^i}{S_{k-1}^i}-\frac{S_{k+1}^i}{S_{k}^i}\right)\quad\text{is constant.} \]
The term in parentheses is positive for all \(i\) and \(k\) because \(S_1^i,S_2^i,S_3^i,\dotsc\) is a logarithmically concave sequence. So there exists a mixed strategy for the searcher that is equally good against every pure strategy of the hider, namely:
\[ p_i=\frac{\left(\frac{S_k^i}{S_{k-1}^i}-\frac{S_{k+1}^i}{S_{k}^i}\right)^{-1}} {\sum_j\left(\frac{S_k^j}{S_{k-1}^j}-\frac{S_{k+1}^j}{S_{k}^j}\right)^{-1}},\quad i=1,\dotsc,n. \]
Clearly, \(A(H)\) must equal \(A(i)\).
This completes an inductive step that the value of the game is \(S_{k+1}/S_k\).
The optimal strategy for the hider is Sod’s Law, which he can implement without being smart.
The optimal strategy for the searcher is to be smart and to choose his next search location with probabilities given above, which depend not only on the set of locations that have not yet been searched, but also on the number of objects that are yet to be found.
Query: What if the hider is smart, but the searcher is dumb?
Is the payoff now different to its value in the other three games? Conjecture: it is now more costly for the searcher to find his objects.
| Hider | ||
| Searcher | Dumb | Smart |
| Dumb | \(v\) | \(>v\) |
| Smart | \(v\) | \(v\) |
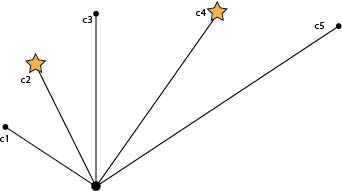
The problem above can be viewed as one of searching for \(k\) objects that are hidden at the ends of a star-shaped graph with \(n\) leaves.

The distances between the middle of the star and the ends of the leaves are \(c_1,\dotsc,c_n\).
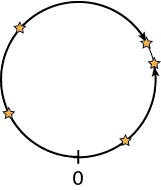
Suppose we allow other graphs. For example, \(k\) objects are hidden around the edge of a \(n\)-gon, or circle with circumference 1.
The searcher starts at some point say 0 and moves along the graph at speed 1. His cost is the total time that it takes to find all \(k\) objects. His search is constrained to be “expanding”, i.e. like “tunnelling”, digging tunnels from his starting point.
In the case of the circle he will, at time \(t\), have tunnelled \(x\) (\(<t\)) clockwise, and \(y=t-x\) counterclockwise, and can extend either \(x\) or \(y\).
A pure strategy for the hider is to hide the object at \(h\) (measured clockwise from \(0\)).
If \(h\) is chosen uniformly on \([0,1]\) it is clear that the expected search time is \[ ET = \int_0^1 P(T\geq t)\,dt = \int_0^1 (1-t)\,dt =1/2. \]
Suppose that the searcher randomly searches the complete circle clockwise or counterclockwise. If the object is at \(h\) his expected search cost will be \[(1/2)h + (1/2)(1-h)=1/2.\]
So the value of this game is \(1/2\).
Hider: hide the object at random.
Searcher: w.p. \(1/2\) search the entire circle clockwise and w.p. \(1/2\) search the entire circle counterclockwise.
Let’s start by assuming the searcher is “dumb”.
We mean that he follows a fixed search path, chosen at time 0 and not modified by when or where he discovers the first object.
Suppose the hider were to hide the two objects independently at random. The cost of a search which searches the entire circle clockwise would be \[ \int_0^1 (1-t^2)\,dt = \frac{2}{3}. \]
But the hider can do better. Suppose the hider hides the objects at \(x\) and \(x+1/2\) where \(x\) is chosen uniformly on \([0,1/2]\).
After time \(1/2\) the searcher will have searched a semi-circle and w.p. 1 have found exactly one object. Its position is uniformly distributed on that semicircle.
The object that is still to be found is uniformly distributed on the complementary semicircle, and so by extending the search it will be found in expected time \(1/4\). The expected search time is \[ \frac{1}{2}+\frac{1}{4}=\frac{3}{4}. \]
If the searcher were to randomize between a complete clockwise and counterclockwise search where should the hider can hide the two objects?
At \(\pm\epsilon\) (measured from 0).
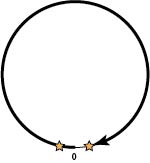
The search cost will be \(1-\epsilon\) (nearly the whole circle).
Suppose instead that the searcher with equal probability of \(1/4\) does one of the following until both objects are found
search the whole circle clockwise
search the whole circle counterclockwise
search half the circle clockwise then the remaining half counterclockwise
search half the circle counterclockwise then the remaining half clockwise
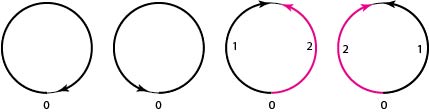
Consider the two halves of the circle, say \(A\) and \(B\).
Each half circle is equally likely to be the last half circle potentially searched, and is equally likely to be searched in the clockwise or counterclockwise direction.
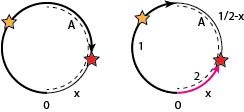
\[ \frac{1}{2}\left( x + \left(\frac{1}{2}-x\right)\right) = \frac{1}{4}. \]
If \(A\) is the last half circle searched and it contains both objects then potentially nearly the whole circle is searched; the expected portion that is not searched might be 0.
But in that case \(B\) contains 0 objects. So if \(B\) is the last half circle potentially to be searched it will in fact not be searched, and so the savings is at least \(1/2\),
So the average savings is \(1/4\), which is also the savings in case 1.
Hence with the posited strategy the searcher has a cost no greater than \(3/4\).
Thus we conclude that the value of this game is \(3/4\).
Lidbetter generalizes these ideas to other graphs and \(k>2\).
Theorem. Suppose the graph has expanding search that never doubles back on itself and ends by returning to 0, (as we can do on a circle).
Then the value of the game (with a dumb searcher) is \((1-\frac{1}{2k})\mu\), where \(\mu\) is the total length of the graph.
This is easier.
It turns out that for \(k=2\) the value of the game is \(2/3\) (\(<3/4\)).
So being “smart” is advantageous.
In general, \(v=1-1/(k+1)\).
We easily see (as Lidbetter explains) that
if the hider simply hides the \(k\) objects independently at random around the circle, then the expected search time will be \(1-1/(k+1)\), and
the following strategy guarantees the searcher an expected search time no more that \(1-1/(k+1)\):
Choose \(j\) uniformly on \(\{0,1,\dotsc,k\}\). Search clockwise until \(j\) objects are found. Then search counterclockwise until all objects are found.
Imagine the objects are located at distances \(x_1<x_2<\cdots<x_k<1\) measured clockwise from \(0\) around the circle.
The expected search time will be
\[ \frac{1}{k+1}\left((1-x_1)\ +\ \sum_{j=1}^{k-1}[x_j + (1-x_{j+1})]\ +\ x_k\right)=\frac{k}{k+1} = v. \]
A squirrel has collected \(r=12\) kg of nuts.
He needs \(s=8\) kg to survive the winter.
Nuts can be hidden in \(n=20\) places, of which a random \(m=10\) will be vandalized (or forgotten).
How should the squirrel hide his nuts (to maximize the probability that the unvandalized locations contain at least \(s=6\) kg nuts)?
two locations with \(6\) kg each?
three locations with \(4\) kg each?
three locations with \(3\), \(4\) and \(5\) kg?
four locations with \(3\) kg each?
five locations with \(2.4\) kg each?
12 locations with \(1\) kg each?
eight locations with \(1\) kg and two locations with \(2\) kg?
In principle we can compute the probabilities and find what is best, but this is tricky to do.
Ruckle’s conjecture is that we can rule out c and f.
(In fact, here a and c are equally good and give probability \(1/2\).)
Ruckle’s Conjecture
For some integer \(k\) (depending on \(r\), \(s\), \(n\) and \(m\)), it is optimal for the squirrel to hide \(r/k\) nuts in each of \(k\) locations. That is, it is never optimal to hide nuts in unequal sized caches.